Time Series Data Compression
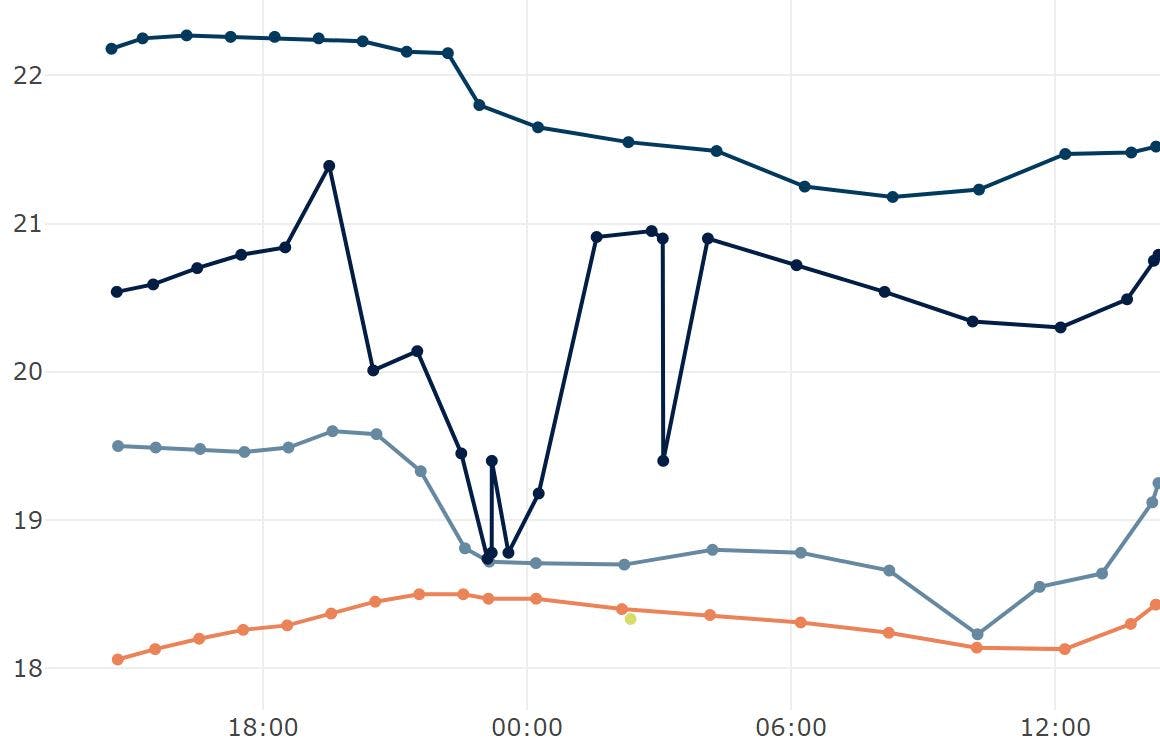
In a previous post I talked about compressing time series-data using a co-linearity test. This approach worked OK but recently I came across a better approach and I've implemented it to reduce the number of data points that are collected for any sensor without losing any of the salient features of the time series data.
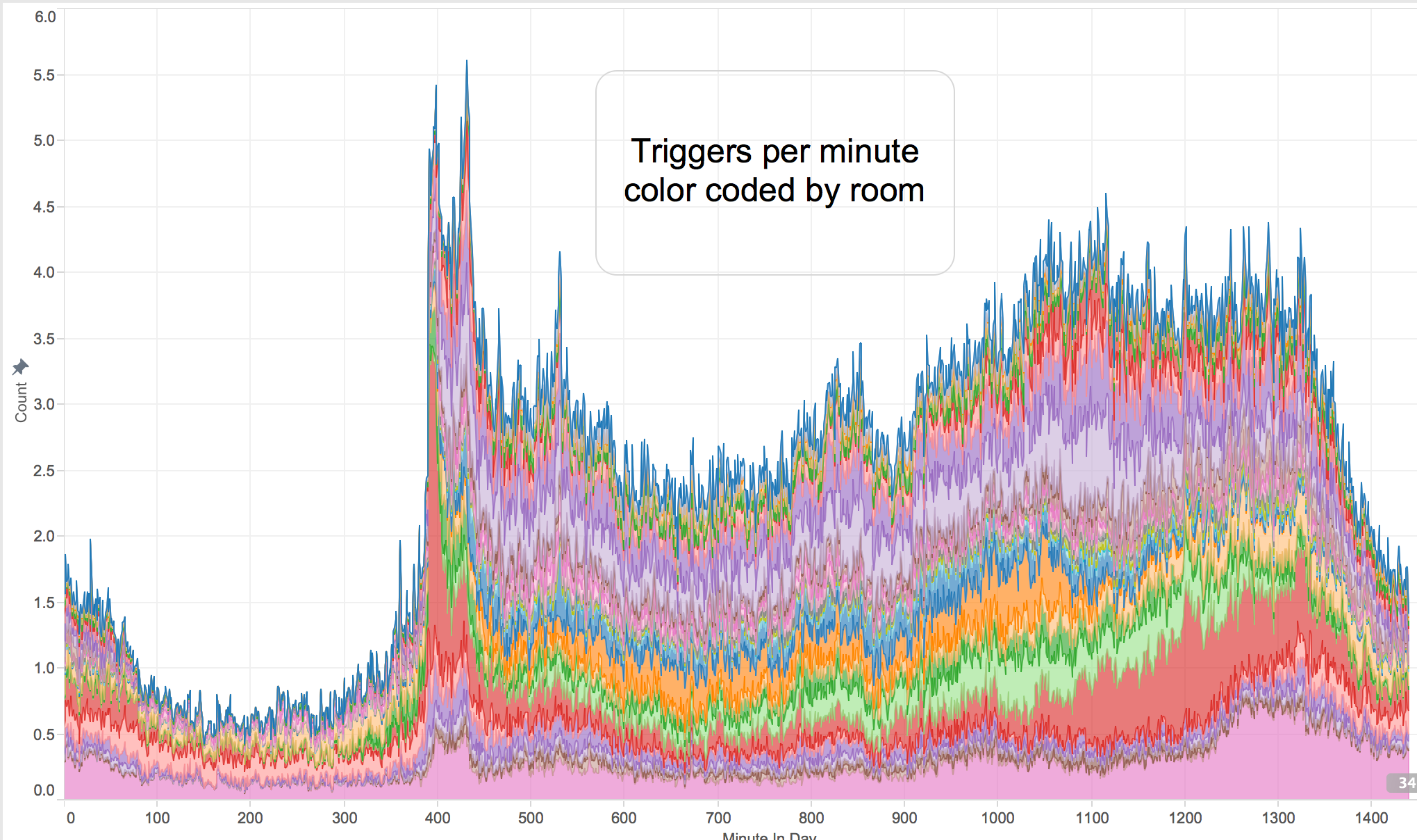
What's needed is an algorithm that preserves the shape of the signal, each local maximum or minimum must be preserved and each inflection point in the curve should be represented. An overall RMS difference between the compressed data and the actual data must be kept small.
I came across this great summary paper: 'An Overview of Moving Object Trajectory Compression Algorithms' which provided some of the ideas behind my latest data compression scheme. In particular a scan or sweep approach to selecting which points to keep or drop.
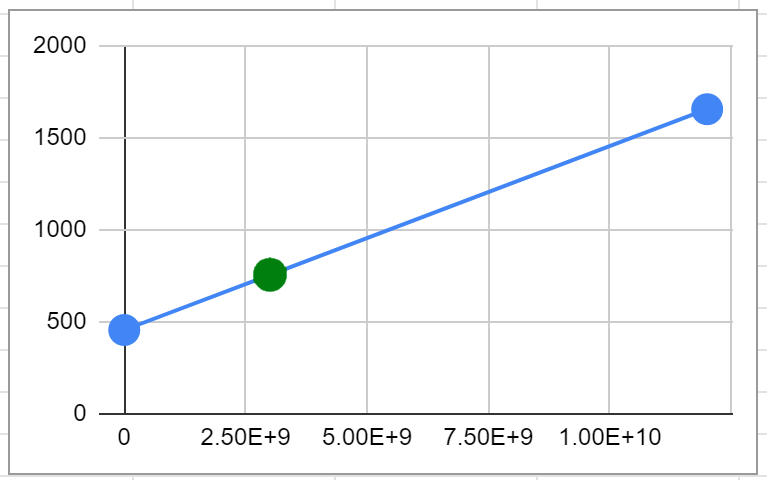
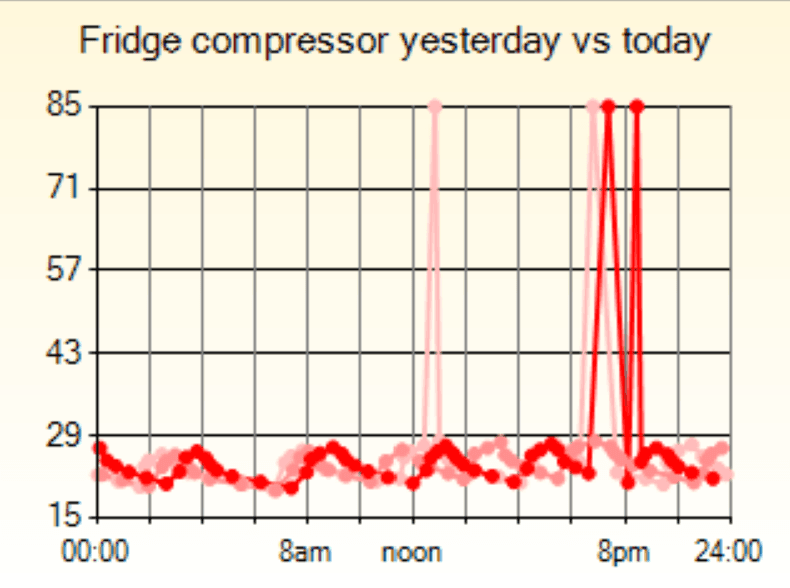
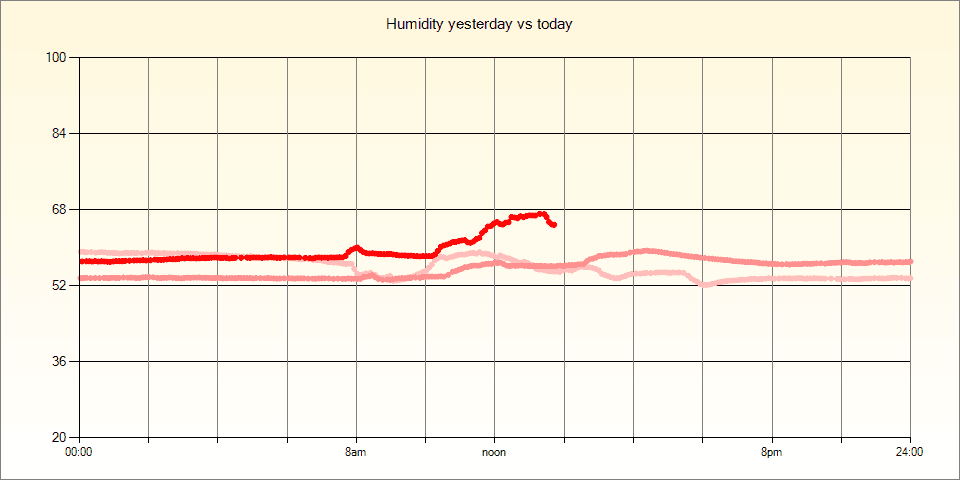
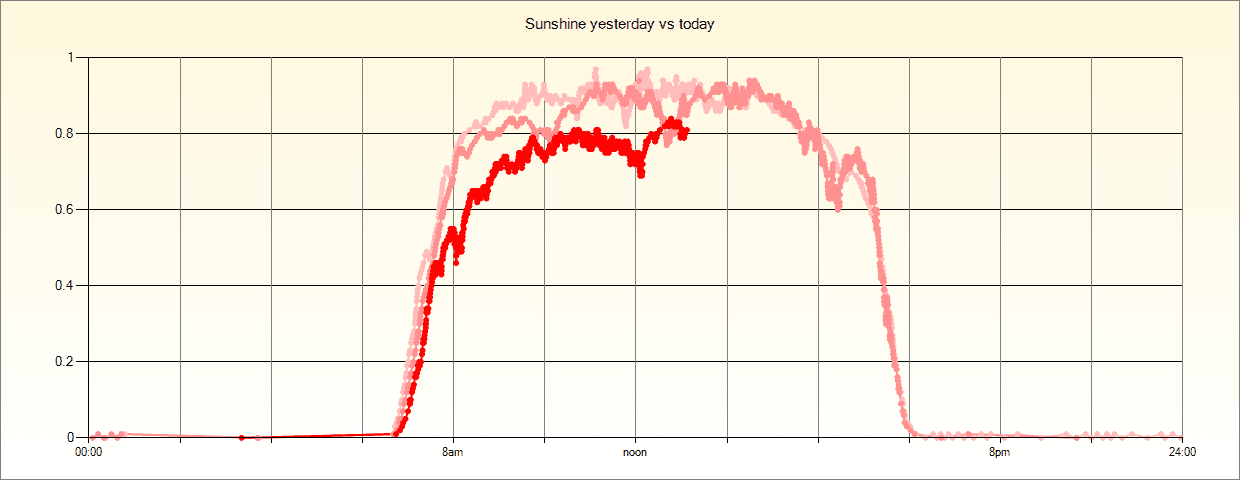
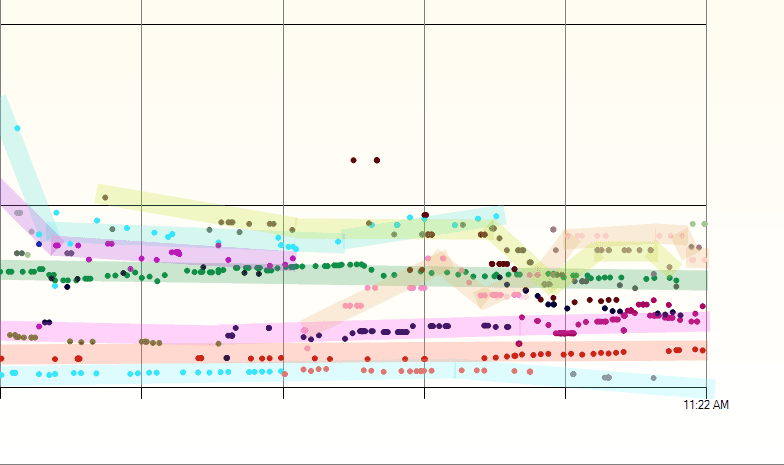
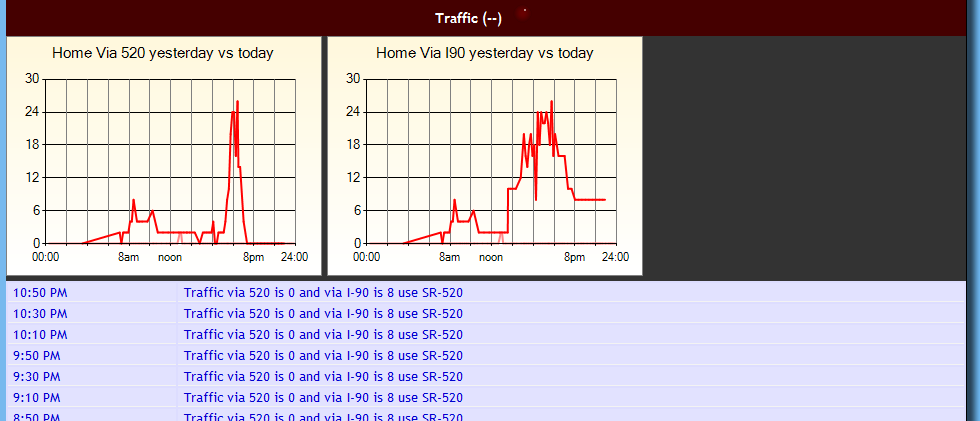
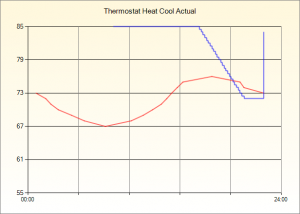
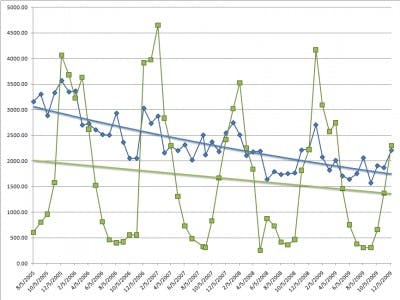
The entire code is below and as you can see on the graph above it does a good job capturing the salient points in the data whilst eliminating as many other points as possible.
To use the code you provide a percentage (e.g. 0.05) which expresses the delta up or down that a point can have from its actual value. At each step the algorithm fits two lines to the data points after the current start point: an upper limit and a lower limit line using the up or down delta calculated from the percentage allowed. As new points arrive, if they are within this 'cone' they replace the previous value and adjust the cone to be narrower based on their location. As that location gets ever further from the start point the cone narrows. If the points stay within the percentage threshold around some line from the start point then they keep removing and replacing the last data point. But as soon as one strays outside the cone, the algorithm keeps the last point before it and the current point and restarts the process with that as the new baseline.
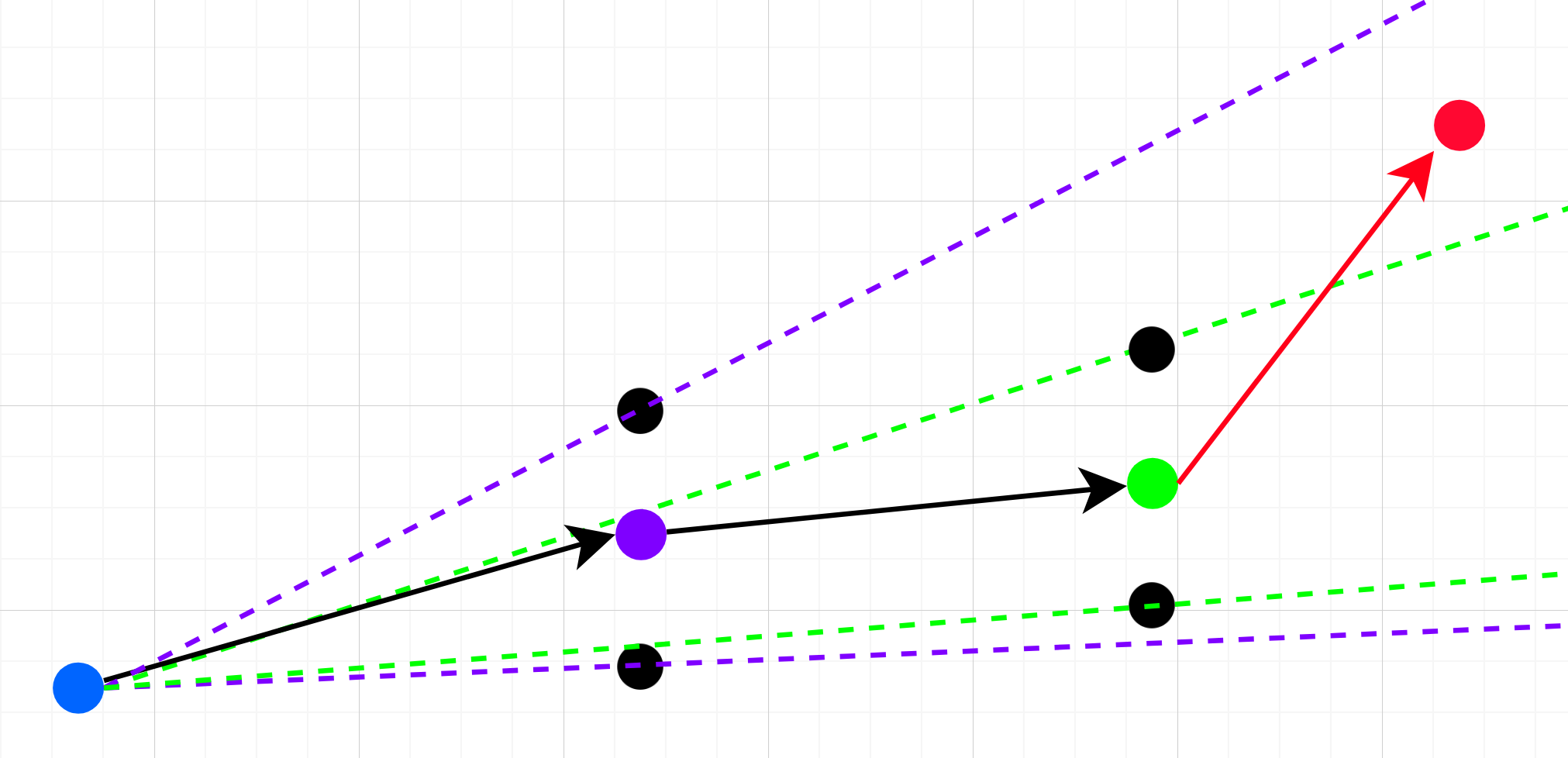
At each inflection point, local minimum, or local maximum, the algorithm saves the current point and starts looking for a new line segment. It turned out to be really simple code and it works really well. To use it you provide two call backs: one to write a value to the database and one to update the last value in the database.
There are other better off-line algorithms for trajectory compression but the beauty of this one is that it works incrementally and only updates the last data point. As such it doesn't need a lot of buffer, can run very efficiently and doesn't change the graph as you are looking at it.
/// <summary>
/// Trajectory compression using narrowing cones
/// </summary>
/// <remarks>
/// Can update last value but can't go further back, resets when the curve changes direction
/// </remarks>
public class TrajectoryCompressor
{
private readonly double percentage;
private double startValue;
private long startTime;
private double previousValue;
private long previousTime;
private bool hasPrevious = false;
private double lower_slope = -1.0;
private double upper_slope = 1.0;
public TrajectoryCompressor(double percentage, long startTime, double startValue)
{
this.percentage = percentage;
this.startTime = startTime;
this.startValue = startValue;
}
public void Add(long timestamp, double value,
Action<long, double> write,
Action<long, long, double> update)
{
if (!hasPrevious)
{
write(timestamp, value);
hasPrevious = true;
previousTime = timestamp;
previousValue = value;
return;
}
if (timestamp == previousTime)
{
// ignore simultaneous values
return;
}
// Add allowed error to it
double upper_estimate = (value > 0) ? value * (1.0 + percentage) : value * (1.0 - percentage);
double lower_estimate = (value > 0) ? value * (1.0 - percentage) : value * (1.0 + percentage);
double upper_bound = (timestamp - startTime) * upper_slope + startValue;
double lower_bound = (timestamp - startTime) * lower_slope + startValue;
bool outside = (value > upper_bound || value < lower_bound);
if (outside)
{
// The new point is outside the cone of allowed values
// so we allow previousValue to stand and start a new segment
startTime = previousTime;
startValue = previousValue;
previousTime = timestamp;
previousValue = value;
hasPrevious = true;
write(timestamp, value); // And write out the current value
// and calculate new min max slope
upper_slope = (upper_estimate - startValue) / (timestamp - startTime);
lower_slope = (lower_estimate - startValue) / (timestamp - startTime);
return;
}
// value is within expected range, it can replace previous
update(previousTime, timestamp, value);
// Keep track of it so we can keep updating
previousTime = timestamp;
previousValue = value;
// and then narrow the allowed range
if (upper_estimate < upper_bound) upper_slope = (upper_estimate - startValue) / (timestamp - startTime);
if (lower_estimate > lower_bound) lower_slope = (lower_estimate - startValue) / (timestamp - startTime);
}
}