The Blog of Ian Mercer.

Filtering techniques

3/3/2021

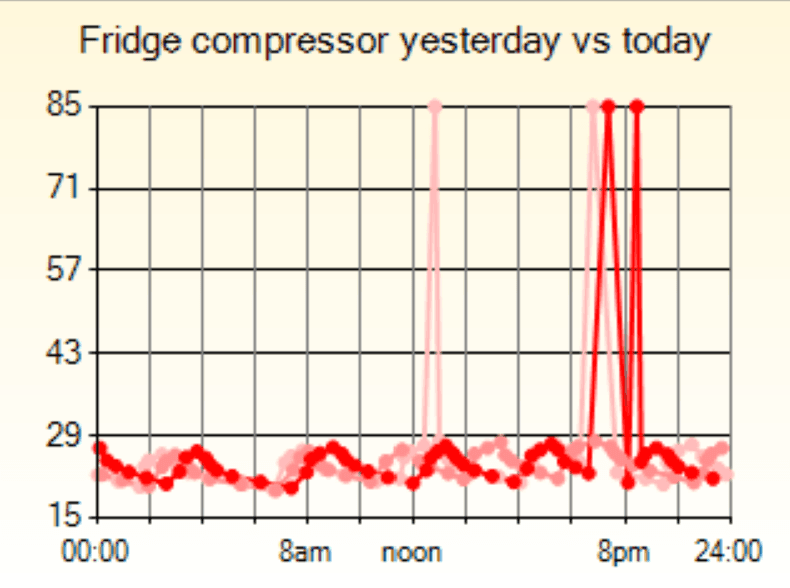
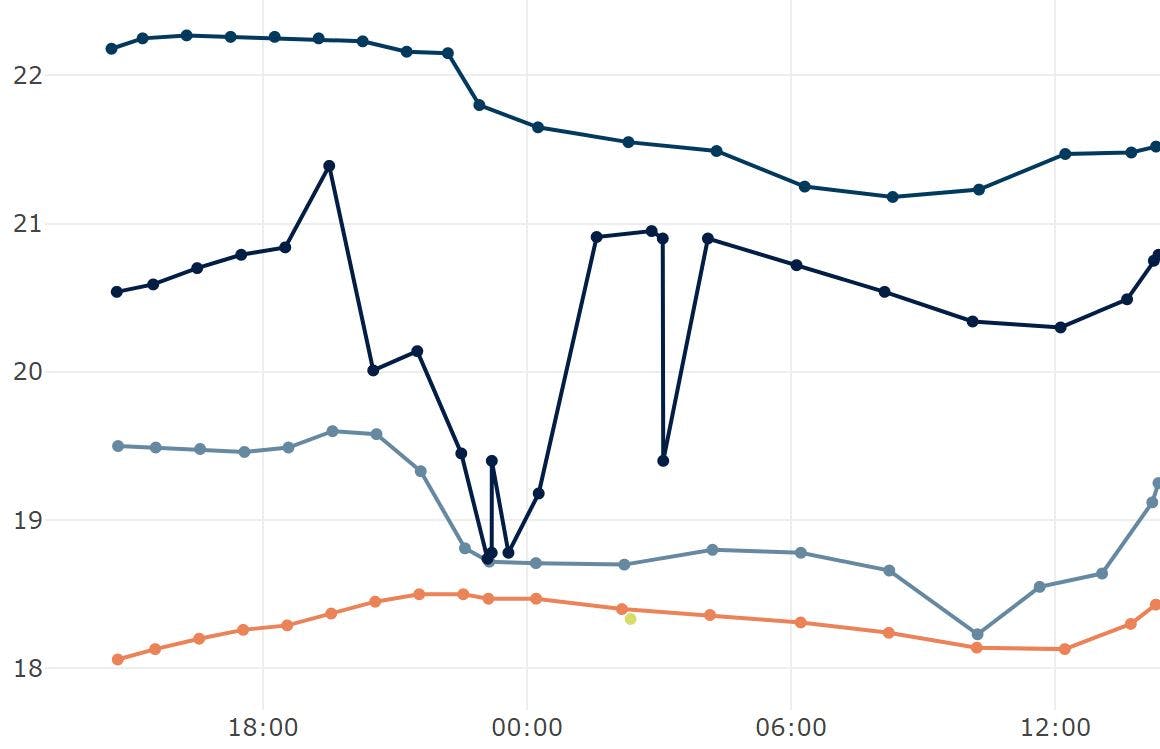
Even the more reliable sensors will glitch occasionally and some of the less reliable sensors will glitch all the time. Filtering sensor data to ensure that these bad values don't get through is essential. Here are some techniques:

Moving Average

This has reasonable results and is very simple to code. You can maintain a circular buffer of values and calculate an average each time you add a new value by averaging all the values in the buffer. In it's simplest for you can keep just one value and do something like:

   current = 0.9 * current + x * 0.1

But it's not great. The glitch values still move the average, and the output lags the input.

Median filter

Instead of taking the average of the buffer, take the median value. This means you need to copy and sort the buffer but that's fairly easy even in C. This approach also lags but it is great for rejecting the occasional stupid spike.

Kalman filter

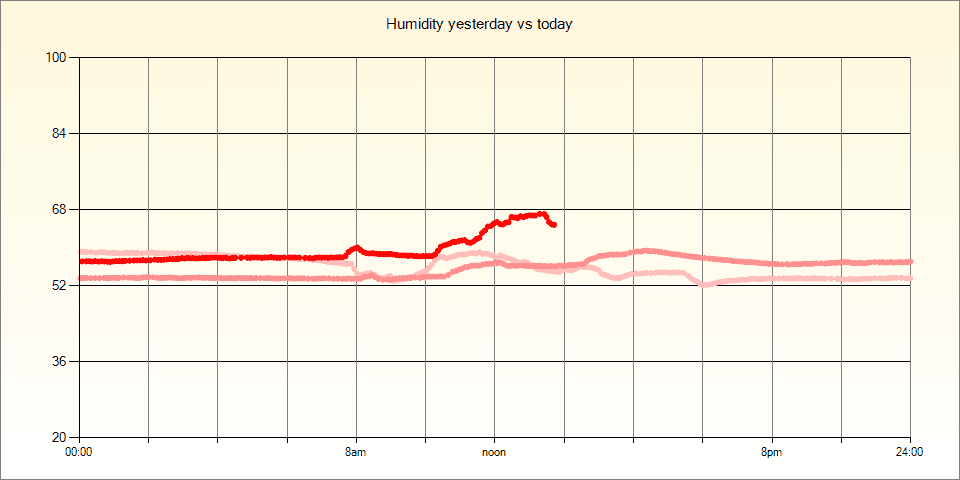
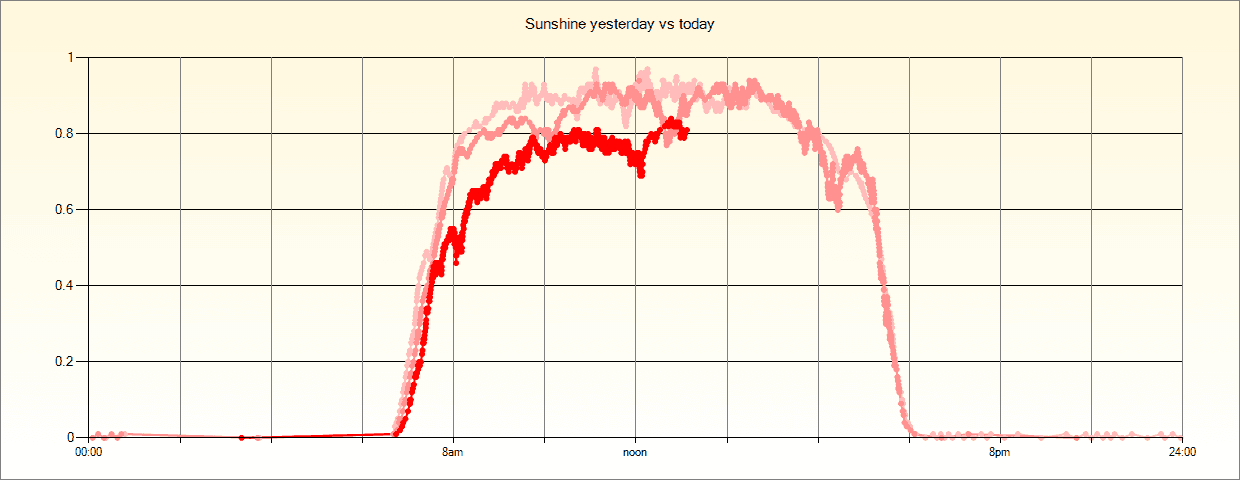
The Kalman filter is a bit harder to understand but essentially it works a bit like a moving average but it also learns how much of the new value to bring in each time and how much of the old value to maintain. It can also operate on multidimensional data.

Recommendation

In addition to rejecting just plain stupid outliers (e.g. 212 degrees for an indoor temperature), I recommend a small median filter to reject outliers followed by a kalman filter for most situations.

Kalman Code (C)

/*
      Kalman filter
*/

struct Kalman
{
    double err_measure;
    double err_estimate;
    double q;
    double current_estimate;
    double last_estimate;
    double kalman_gain;
};

void kalman_initialize(struct Kalman *k)
{
    k->current_estimate = NAN;   // marker value used by time interval check
    k->last_estimate = NAN;      // marker value, so first real value overrides it
    k->err_measure = 10.0;
    k->err_estimate = 10.0;
    k->q = 0.15;   // was 0.25, moved down for more frequent updates
}

float kalman_update(struct Kalman *k, double mea)
{
    // First time through, use the measured value as the actual value
    if (isnan(k->last_estimate))
    {
        k->last_estimate = mea;
        k->current_estimate = mea;
        return mea;
    }

    k->kalman_gain = k->err_estimate / (k->err_estimate + k->err_measure);
    k->current_estimate = k->last_estimate + 
        k->kalman_gain * (mea - k->last_estimate);
    k->err_estimate = (1.0 - k->kalman_gain) * k->err_estimate + 
        fabs(k->last_estimate - k->current_estimate) * k->q;
    k->last_estimate = k->current_estimate;

    return k->current_estimate;
}