N-Gram Analysis of Sensor Events in Home Automation
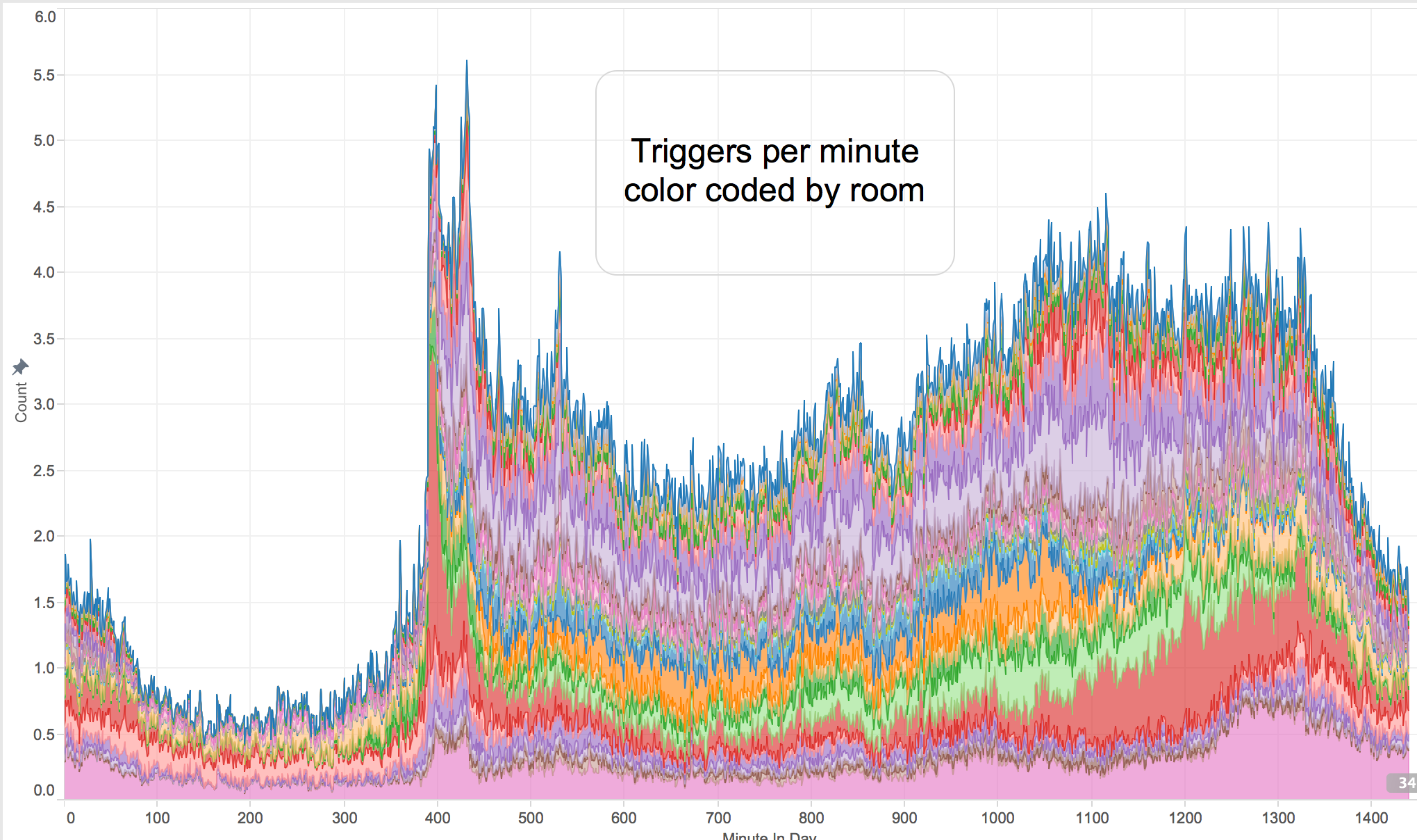
This week I decided to add some visualizations of the ever growing database of sensor data my house is accumulating. The first visualization I attempted was a N-gram analysis (actually just a digram, n=2). I created a quick autocomplete API method for picking sensors, an Angular.js form for the UI and another API that given a pair of sensors, scans the entire database to build a new collection containing delta values from when one sensor is triggered to when the next is triggered. The API returns a null collection until the background scan has completed so the UI can display a working indicator and finally when the results are available it can show the graph. For the graph itself I used D3.js which provides methods to aggregate frequency values into buckets (histogram) and then I display that histogram as a line using one of the many interpolations offered.
Here are some of the interesting graphs this technique has produced.
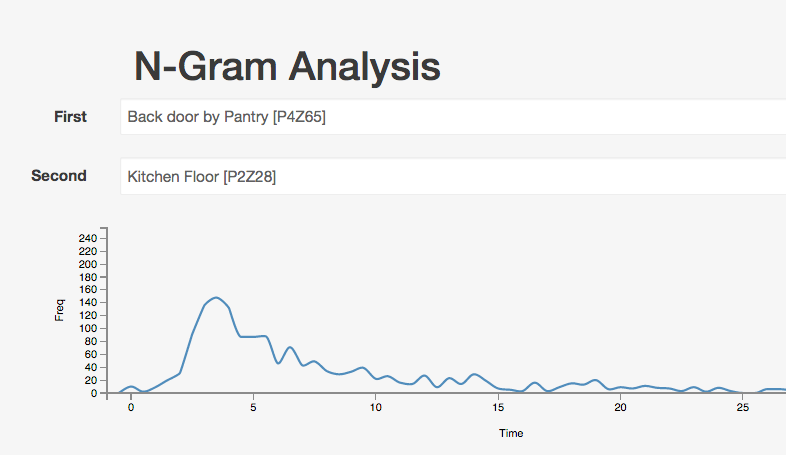
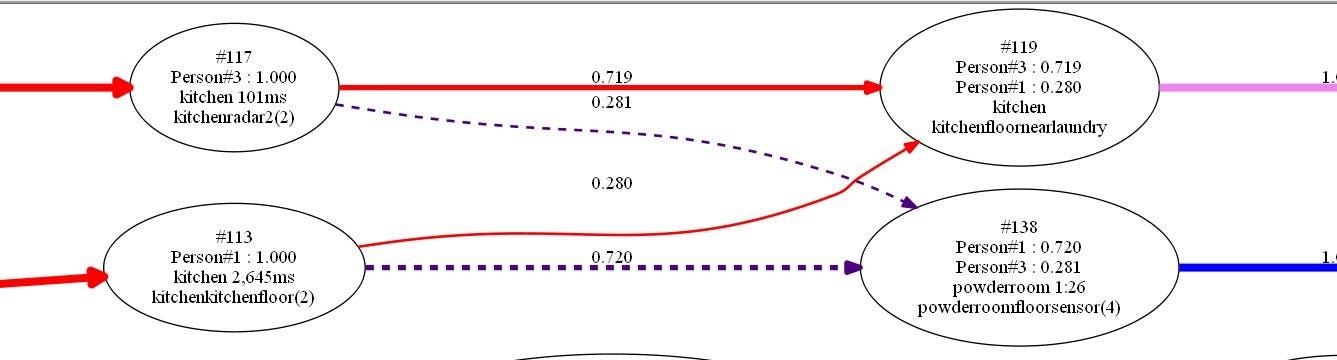
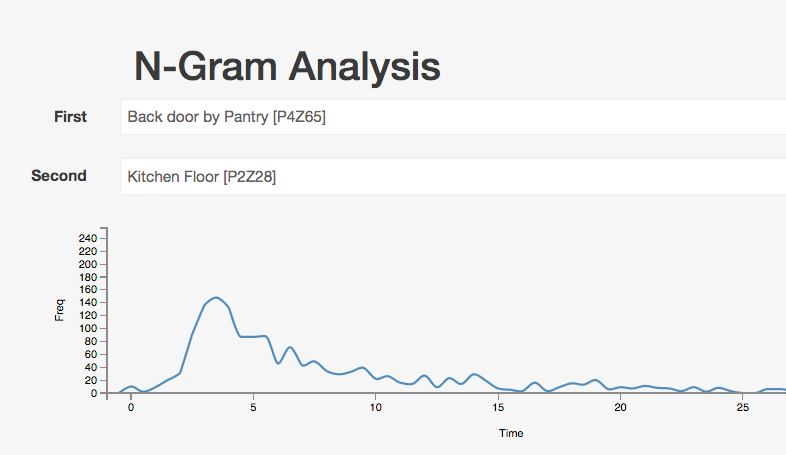
This one shows how long it takes someone to get from the back door into the kitchen. Just a few seconds typically.
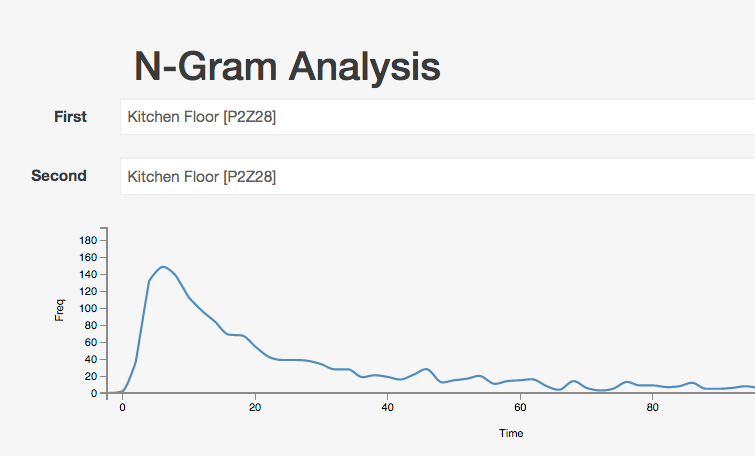
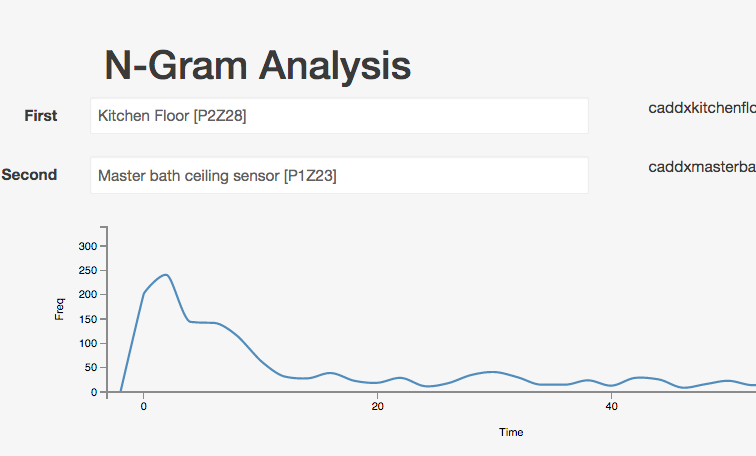
This one shows the gap between repeated triggers of the kitchen floor.
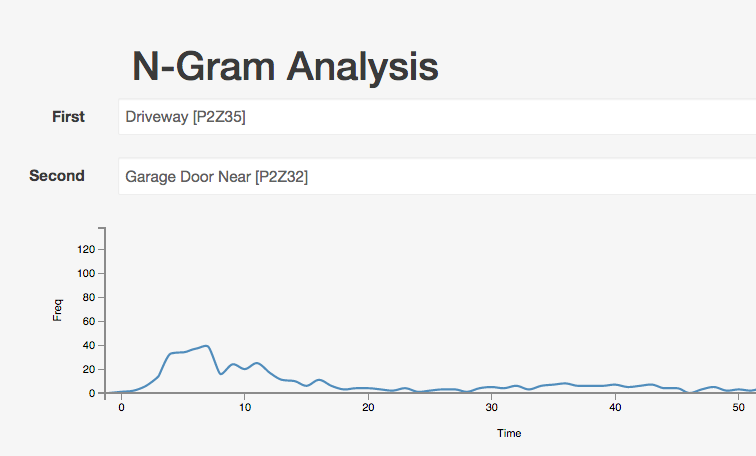
It takes about 8 seconds from a car passing through the gate until the garage door starts opening. But it's nowhere near as smooth a curve and it has a much longer tail.
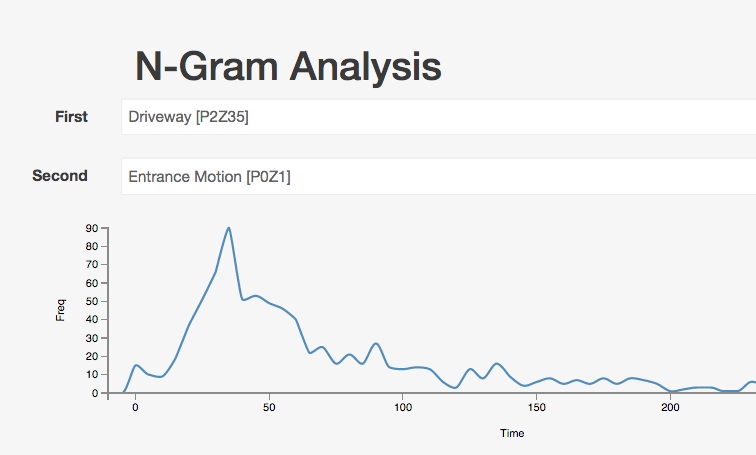
When we have visitors or deliveries they come to the front door where there is a motion sensors. It takes about 35 seconds from a car passing through the gate until motion is detected on the front door step.
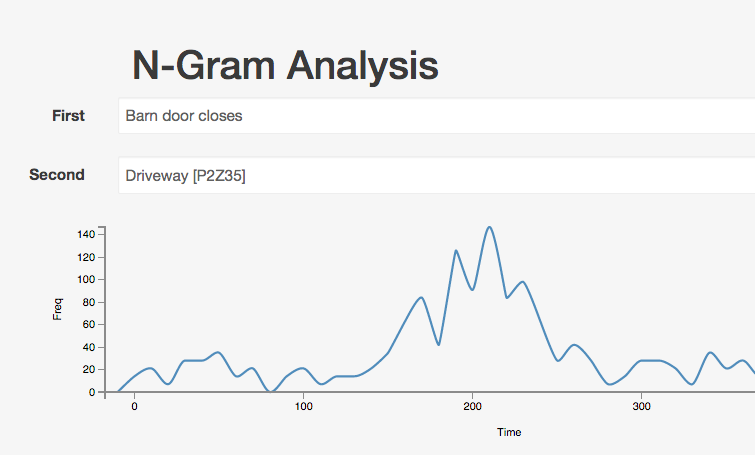
It takes about 3 minutes to drive a car around the block from the barn to the house. The three spikes around this value might represent the three different drivers in the family and the way they drive, or there could be some other reason why the journey time varies this way (assuming they are even statistically significant - which I haven't checked).
One challenge in interpreting these results is that even two unrelated sensors have a nice exponential graph, although the peak around zero seconds is a clear indication that these are not related since they are impossibly close in time.
Next Steps
These graphs have immediately given me a way to fine tune some of the it-this-and-then-that-within-30-seconds type of logic I sometimes use. I now have an accurate understanding of the likely distribution of times between two events.
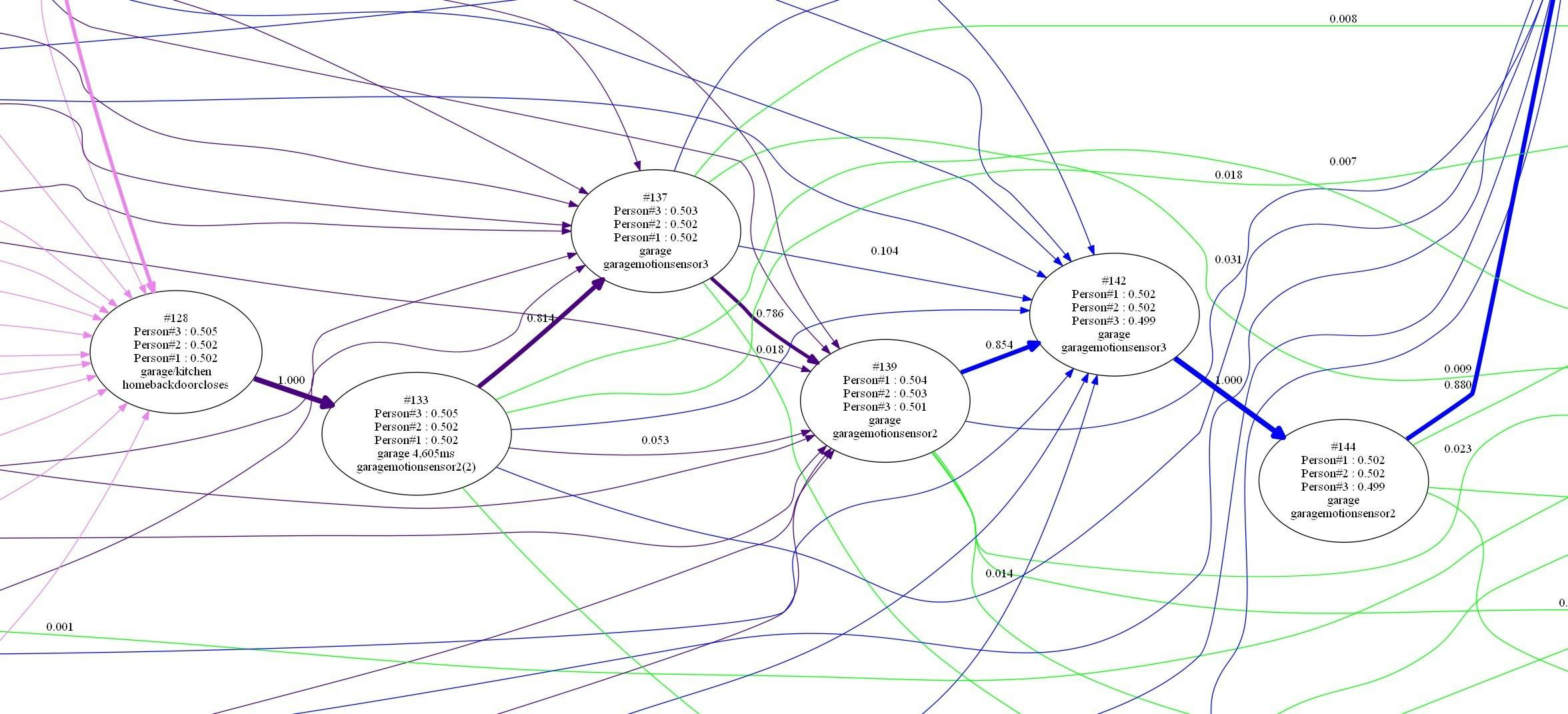
Given a sufficiently dense network of sensors it should be possible to deduce the geometry of the house without being given any information about where the sensors are located.
By feeding all of these Digrams back into the system as sensors I can start looking for interesting 3-grams and 4-grams.
I'm also considering having the software scan all of the digrams to decide which are 'interesting' so it can present a list of suggested sensor pairs, e.g. "Is living room floor then front door an interesting event?" Using the graph of the house I can get the system to compute all possible 2-Grams that are physically likely, i.e. the sensors are in rooms that are connected to each other within a reasonable distance. The graph will, once again prove to be a very useful representation of the house.