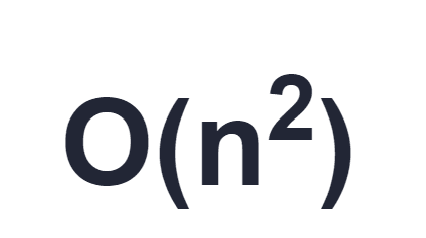Cache optimized scanning of pairwise combinations of values

Suppose you wanted to calculate all of the pairwise combinations of the values in a vector of n elements. The result would be a 2D matrix of dimensions n squared. A naive approach to this would be two nested for loops evaluating each of the n squared values. But now suppose that the values in the source vector are actually really large objects, too large to hold all of them in memory and you need to page them in from disk as necessary, caching maybe just a few of them.
If you take the naive approach to this you will thrash the cache, every single calculation will result in a cache miss, and a disk access.
So I went looking for a way to improve the cache hits by ordering the data in a better order and here's what I found:
Various space-filling curves such as the Z-Curve, The Peano Curve, a Hilbert Curve exist that can turn a 2D space into an ordered list of items such that items along the list are close spatially.
Applying a simple Z-curve to the problem improved the cache hit rate by 6x in my case!
The same techniques can be applied to in-memory data structures to try to keep them in the CPU cache.